PÉRDIDAS MAGNÉTICAS
Introducción
La variación del campo magnético en un material origina efectos no deseados, como las pérdidas de energía debidas a las corrientes de Foucault que se disipan en forma de calor, las pérdidas por histéresis en el ciclo B-H de magnetización-desmagnetización y, en el caso de dispositivos electromagnéticos, distorsiones en las formas de onda debidas a la no linealidad de la relación B-H.
Subir
Curva de magnetización
Se denomina curva de magnetización de un material, o característica magnética, a la representación cartesiana de los valores de la inducción magnética B (en ordenadas) y de la excitación magnética H (en abscisas), como se muestra en la Figura 1. En ocasiones se representa la imanación M en lugar de la inducción B.

Figura 1
Supóngase un núcleo ferromagnético de un transformador, si se le aplica una excitación magnética H, surgirá una inducción B. Si aumentamos la excitación magnética progresivamente desde cero (aumentando la intensidad) y se representa la curva de magnetización, se observa que la inducción es proporcional a H y que el tramo oa (Figura 1) es prácticamente recto. Esto se debe a que la permeabilidad es constante y alta (cuanto más alta es la permeabilidad más vertical será la gráfica en este tramo).
Llegados al punto a la grafica deja de ser lineal, o lo que es lo mismo, la permeabilidad deja de ser constante. A este tramo ab se le denomina codo de saturación. Alcanzado el punto b la grafica vuelve a ser lineal. En el tramo bc el material está completamente saturado. Esta saturación supone que para grandes aumentos de la excitación no se detectan cambios significativos de la inducción B. En esta zona el material tiene baja permeabilidad (se comporta prácticamente como el aire).
A nivel molecular, lo que sucede en los materiales ferromagnéticos es que al aplicarles un campo los momentos magnéticos de los dominios se orientan con él a medida que este aumenta (tramo ab). Una vez alineados con el campo se alcanza la saturación del material (a partir de b) lo que supone que no existen más dominios que puedan contribuir a la inducción o magnetización del material. Por esta razón, una vez saturado el material, el valor de la inducción prácticamente no varía.
Para un mejor aprovechamiento del material (mínima sección) los núcleos de las maquinas se diseñan para que, con sus valores nominales de funcionamiento, trabajen cerca del comienzo del punto a (codo de saturación). Subir
Ciclo de histéresis
En el apartado anterior se explicó qué ocurre cuando a un material desmagnetizado se le aplica un campo. Pero, ¿qué ocurre si aumentamos y disminuimos este campo sucesivas veces de forma cíclica?
En un material ferromagnético se vió que al retirarle el campo aplicado no vuelve a su estado original ya que conserva un magnetismo remanente. Por lo tanto, si partiendo del punto del punto c de la Figura 1, se disminuye el valor de la excitación hasta anularla se observa que la nueva grafica no coincide con la inicial (Figura 2). Puede observarse que en ausencia de excitación (H=0) el valor de la inducción no toma un valor nulo si no que viene dado por el valor del tramo OD en ordenadas. Este valor se conoce como magnetismo remanente.

Figura 2
Este magnetismo remanente lo originan los momentos magnéticos de los dominios del material que no vuelven al estado original después de retirar el campo aplicado, sino que quedan parcialmente orientados. Todos los materiales ferromagnéticos presentan un cierto grado de magnetismo remanente, algo que es de especial importancia en las maquinas eléctricas.
Si ahora se continua disminuyendo el valor de H (invirtiéndolo), se llega a un estado determinado por el punto E (Figura 3). En dicho punto el magnetismo remanente se anula, para ello es necesario aplicar una excitación o fuerza magneto motriz (f.m.m) de valor EO. Este valor se denomina fuerza coercitiva. Si ahora se anula la excitación, el material queda desimantado (la suma neta de los momentos de los dominios del material es cero). 
Figura 3
Si en lugar de anular la excitación, la seguimos aumentando, se produce un campo inverso al anterior con valores de inducción B negativos (Figura 4). Aumentando el valor de campo se produce el mismo efecto descrito anteriormente. En un primer tramo, para aumentos pequeños de H se producen grandes aumentos de B, este tramo se mantiene hasta alcanzar, de nuevo, el codo de saturación y, posteriormente, la saturación del material en el punto F.

Figura 4
Si nuevamente se disminuyo el módulo de la excitación magnética hasta anularla (Figura 5), es vuelve a tener un magnetismo remanente dado por OG , similar al OD obtenido anteriormente, pero de sentido opuesto.

Figura 5
Ahora, aumentando la excitación de nuevo, se llega al punto I (Figura 6) donde, con una excitación OI, se vuelve a desmagnetizar el material.
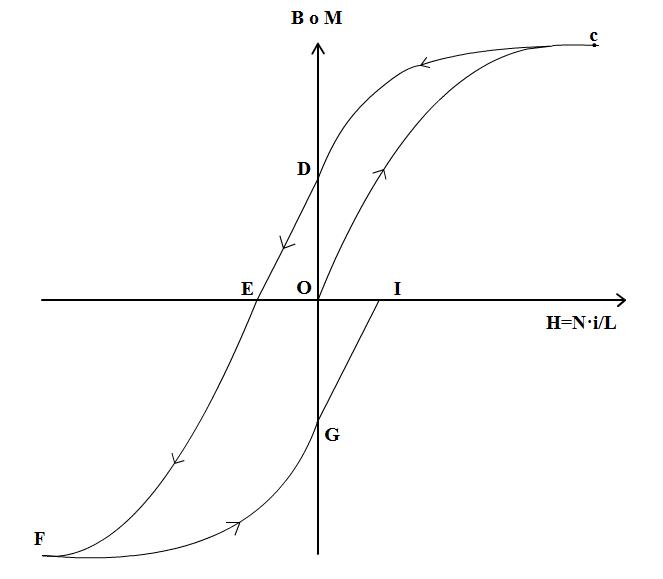
Figura 6
Finalmente, aumentando más la excitación, se vuelve al punto de saturación C en el que se cierra el ciclo (Figura 7). Se obtiene, así, la característica magnética completa, cuya forma recibe el nombre de ciclo de histéresis magnética. 
Figura 7
Este ciclo de histéresis se obtiene, por ejemplo, en el núcleo de los transformadores ya que funcionan con una excitación sinusoidal (valores de tensión y corriente sinusoidales).
Cabe destacar que un mismo material puede tener varios ciclos de histéresis dependiendo del valor de la excitación máxima y mínimo que se aplique. El ciclo de histéresis magnético está íntimamente ligado a la estructura de dominios presente en el material. Así como la imanación de saturación queda determinada únicamente por el material magnético estudiado, parámetros tales como la imanación remanente ó el campo coercitivo dependen, no solo de material, si no también de su microestructura, tamaño de grano y presencia de defectos, y de su relación con los dominios magnéticos.
Según su ciclo de histéresis, los materiales se pueden clasificar en:
• Materiales magnéticos duros: Los materiales magnéticos duros se caracterizan por una alta fuerza coercitiva Hc y una alta inducción magnética remanente Br (Figura 8), de este modo, los ciclos de histéresis de estos materiales son anchos y altos. Estos materiales, una vez se imantan, son difíciles de desimanar, por ello se utilizan para fabricar imanes artificiales.

Figura 8: Curva de histéresis de un material magnético duro.
• Materiales magnéticos blandos: Los materiales magnéticos blandos se imanan y desimanan fácilmente, por lo que presentan curvas de histéresis de apariencia estrecha con bajos valores de fuerza coercitiva (Hc) y alta saturación (Figura 9). Por tanto, tienen permeabilidades magnéticas altas. El uso de estos materiales está centrado en núcleos para transformadores, motores, generadores…
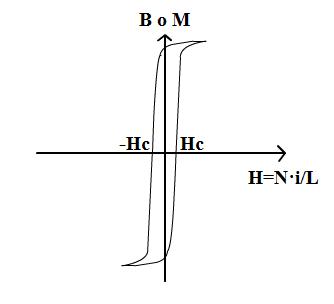
Figura 9: Curva de histéresis de un material magnético blando.
Subir
Pérdidas por histéresis magnética
El proceso de magnetización y desmagnetización descrito anteriormente provoca calentamientos en el material que indican disipación de energía. Estas pérdidas se deben a la diferencia entre la energía transferida al campo durante la magnetización y la que se devuelve en la desmagnetización. Se ha demostrado que el valor de estas pérdidas coincide con el área encerrada por el contorno del ciclo de histéresis (Figura 10).
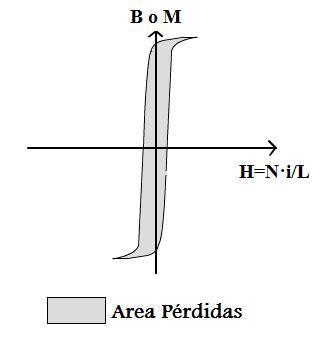 
Figura 10:
Representación del área de pérdidas en materiales blandos (izquierda) y duros (derecha)
De la Figura 10 se puede extraer el motivo por el cual para máquinas eléctricas se suele introducir núcleos de materiales blandos, ya que tienen menores pérdidas por histéresis que los duros, por tanto, no sufren tanto calentamiento y el rendimiento de la máquina es superior.
El cálculo numérico de estas aéreas no es sencillo, ya que se necesita conocer la ecuación de las curvas implicadas en la representación del ciclo de histéresis. Por ello, para este cálculo suele utilizarse la ecuación 1, que se conoce como ecuación de Steinmetz.
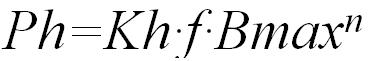 (1) (1)
Donde Ph es el valor de las pérdidas por histéresis, f la frecuencia de la señal de excitación, Kh es una constante que depende del material (puede estar entre 0.001 para un buen acero al silicio y 0.03 para el acero fundido duro). Bmax es el valor de la inducción máxima y n toma el valor de 1.6 para inducciones inferiores a 1 Tesla y 2 para inducciones superiores.
Las unidades de las perdidas por histéresis son los Vatios por metro cuadrado (W/m²). Subir
Foucault
Las pérdidas de Foucault se deben a las corrientes inducidas sobre el material ferromagnético como consecuencia de estar sometido a un campo magnético variable con el tiempo. Dichas corrientes reciben, también, los nombres de corrientes parásitas o de remolino. Si el material magnético es aislante, como es el caso de las ferritas, estas pérdidas son nulas.

Figura 11
La dirección de las corrientes de foucault viene dada por la regla de la mano derecha, agarrando el vector campo con la mano derecha y el pulgar apuntando en su dirección, el resto de los dedos marcan la dirección de las corrientes parasitas (Figura 11).
EL módulo de la pérdidas de Foucault viene determinado por la ecuación 2, en donde Kf es una constante proporcionada por el fabricante para cada tipo de chapa, f es la frecuencia a la que trabajará el circuito magnético y Bmax la inducción máxima que se puede presentar. De esta ecuación se deduce que las pérdidas son proporcionales al cuadrado de la frecuencia y la inducción máxima, siendo estas dos magnitudes dependientes del tipo de excitación de la bobina que actúa sobre el circuito magnético. 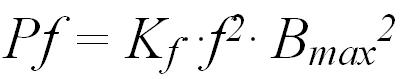 (2) (2)
Las pérdidas de Foucault se miden en W/kg y, en la práctica, suelen darse las pérdidas magnéticas totales, determinadas experimentalmente, en forma de tablas o gráficos.
Subir
|